LET'S REPAIR AND MODERNIZE THE SHARPE RATIO
Fundamental problems with Modern Portfolio Theory and the mean-variance paradigm
Since first published by Harry Markowitz in 1952, millions of investors, directly or through their advisors or portfolio managers, have relied upon a particular analysis of portfolio risk and returns to make their investment decisions. Modern Portfolio Theory (MPT), and its components (mean return, variance, beta, etc.) are widely-accepted as the state of the science in portfolio management, but there are critical flaws in the method that must be addressed. Herein, we attempt to solve a few of the fundamental issues with MPT and its most popular measure, the Sharpe Ratio:
Let's dive in.
- Average (arithmetic mean) of returns can be highly misleading.
- Variance and standard deviation are not identities of, nor analogies for, risk.
- Placing two measurements into a ratio can be distortive. Changes in the numerator (mean returns) move the ratio linearly, while changes in the denominator (standard deviation of returns) move the ratio hyperbolically. This leads to a sometimes unhelpful bias to funds with lower returns and lower variance. A fund with no variability of returns, has an infinite Sharpe Ratio, regardless of return. That is not helpful to the analysis.
- A comparison to an index may yield misleading results, as any negative correlation, which may be desirable for the investor, increases the variance, thus lowering the Sharpe Ratio. A comparison to a risk-free investment does not have this limitation, as such typically has no variance.
Let's dive in.
The Sharpe Ratio
First introduced by William F. Sharpe in 1966, the Sharpe Ratio is a measure of the expected return (reward) of an investment, versus the amount of variability (MPT proxy for risk) in the return. Since its revision in 1994, the Sharpe ratio has taken on 2 general forms: the ex-ante (prediction of future return and variance), and ex-post (analysis of past return and variance). For the most part, ex-ante predictions are simply hopeful guesses, or estimates patterned after observations of past performance of similar investment vehicles. In either case, ex-post observations are the most critical determinations in constructing the Sharpe Ratio. For that reason, we will focus here on the ex-post Sharpe Ratio.Let's walk through the derivation of the Sharpe Ratio. (Don't be discouraged if you don't understand the mathematics; We'll try to explain as we go along.) The ex-post Sharpe Ratio measures how high the returns were, versus how varied those returns were. More specifically, it is the ratio of the differential returns (difference between the returns of the investment and a benchmark investment) versus the historic variability (as standard deviation) of those returns. Some select a "risk-free" investment (treasury bond) as the benchmark, while others choose an index like the S&P 500. Because an index of securities has its own variability, which, in calculating the difference of returns, are indistinguishable from the variability of the fund, we choose to use the risk free rate in our study. Here is the Sharpe Ratio derivation [from Sharpe, 1994], then explanation below:
$D_t ≡ R_{Ft} - R_{Bt}$
$D_t$
$R_{Ft}$
$R_{Bt}$
$R_{Ft}$
$R_{Bt}$
- the differential return in period t, is defined as
- the return of the investment (fund) in period t, minus
- the return of the benchmark in period t.
- the return of the investment (fund) in period t, minus
- the return of the benchmark in period t.
$D↖{-} ≡ 1/T ∑↖T↙{t=1} D_t$
$D↖{-}$
- the average value (arithmetic mean) of the above differential returns
(Mean is the "first moment" of statistical analysis. It is the "average" of the values.)
$σ_D ≡ √{ {∑↖T↙{t=1} (D_t - D↖{-})^2} / {T-1} }$
$σ_D$
- standard deviation of differential returns
(Variance is the "second moment" of statistical analysis. Standard Deviation in the square root of Variance. They are measures of how "varied" the values are, or how far they stray from the average.)
$S_h ≡ D↖{-}/σ_D$
$S_h$
- historic (ex-post) Sharpe Ratio. Mean divided by standard deviation
Why did we go through this exercise? We wanted to show you the components of the Sharpe Ratio, and how it is constructed, so we can then demonstrate our methods for improving it. To calculate the Sharpe Ratio, one must first calculate the returns per sub-period of the investment, compare them to a benchmark during the same sub-period, and calculate the difference. Then, the average of the differences is divided by the standard deviation (variability, or noise) of those differences. For example, let's say one wanted to calculate the Sharpe Ratio for a fund over one year, and uses the monthly returns for the sub-periods. In a spreadsheet, one would put the monthly returns of the fund in one column, the monthly returns of the benchmark investment in another column, and calculate the difference between the two for a third column. Using this column of differences, one would find the average and the standard deviation, and calculate the ratio. It is far more simple than it appears in the mathematics above; Most spreadsheet programs will calculate the mean and standard deviation for you.
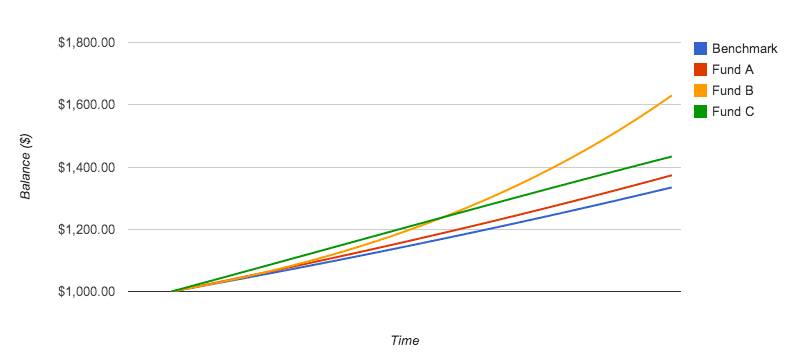
Problem #1
Why is this a potential problem? First, because a simple arithmetic mean (average) of return percentages can be misleading. Return percentages are not additive. For example, consider the following funds:| Fund #1. | Periodic returns: 10%, 5%, -5%, -10%. | Average return: 0% |
| Fund #2. | Periodic returns: 90%, 50%, -50%, -90%. | Average return: 0% |
These two funds would be indistinguishable were one only to look at the average returns. However, the realized returns are quite different. At the end of these four periods, the total return of Fund #1 is -1.25% ((1.10 * 1.05 * 0.95 * 0.90) - 1), while the total return for Fund #2 is -85.75% ((1.90 * 1.50 * 0.50 * 0.10) - 1). In neither case does the average return reflect a losing investment, nor make any distinction between these two quite different funds. Simple arithmetic averages, when dealing with return percentages, can be wildly inaccurate.
Consider these funds:
Our solution to this problem is outlined below, but let's continue identifying issues that need to be addressed...
Problem #2
Consider these funds: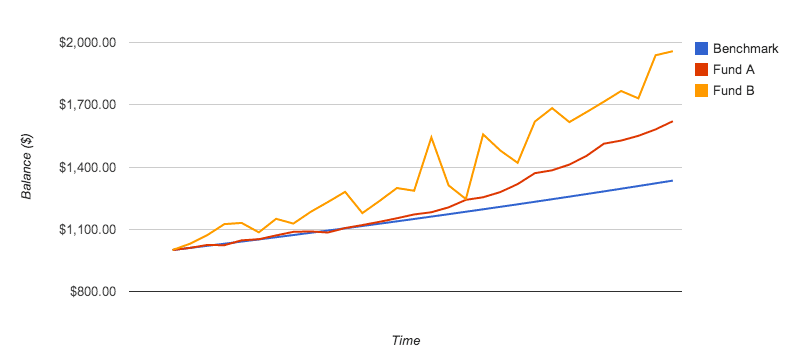
As an aside, an investor could choose two high-return, high-variability funds that are negatively correlated. That would have the benefit of adding return to the portfolio, while counterbalancing variability. Reliance on the Sharpe Ratio alone does not facilitate selection of such funds.
Consider these funds:
This serves as a nice segue into another issue, so let's get this out of the way:
Problem #3
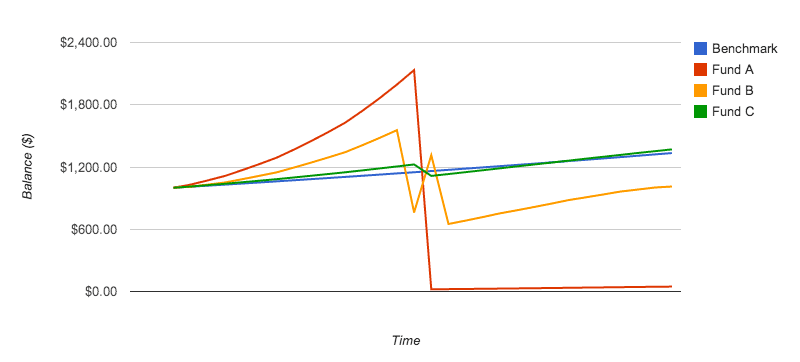
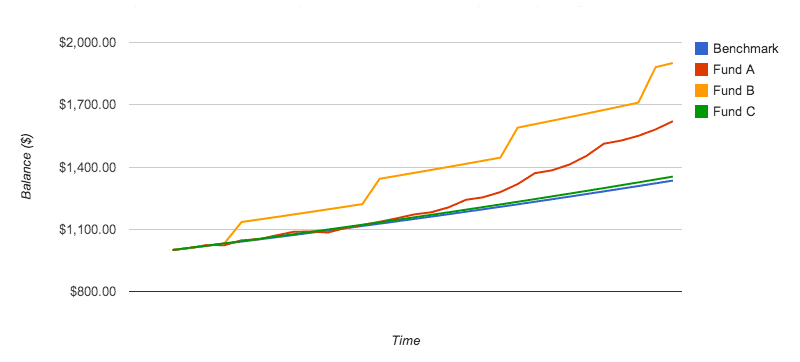
Variability is not an identity for, nor an analogy to, risk. Consider these funds: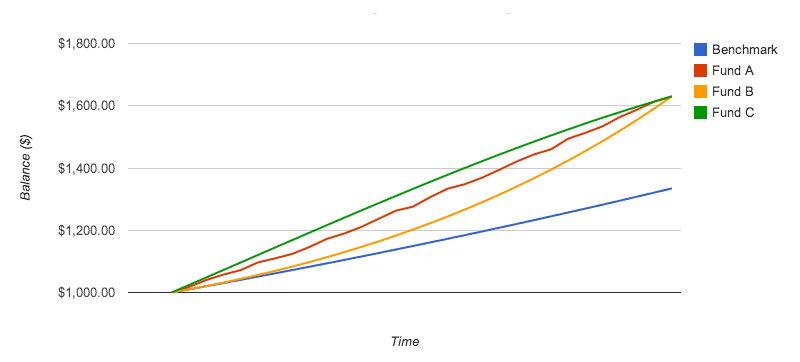
Which of these funds would be most favorable going forward? Which is most risky? Many investors believe that, during short sample periods, returns are random, with prices moving in Brownian motion fashion. Thus, each of the returns shown would be equally likely, alternative histories, with the same probability of occurrence. As such, they would be indistinguishable from one another, as far as probability of returns going forward, and each would have the same risk. But, is that truly the case?
Over time, prices and returns are not random; They are intentional. Countless man-hours are invested daily in efforts to increase capital, asset, and security prices. Without correlating results, humankind would have stopped producing long ago. Fund A's returns appear healthy, and its variability could be explained by seasonality, temporary changes in the marketplace, or randomness. Fund C's returns could also be random. However, knowing that the executives and employees of the companies in that fund are making every effort to grow earnings, the declining rate of returns is troubling. Despite their best intentions, it appears that they are failing to grow returns consistently. It is not unsound reasoning to reject Fund C, especially since funds with more favorable growth trends are available. Fund B appears to be most healthy. The efforts of its participants are succeeding in moving rates of return higher. Thus, in light of the possibility of a random walk, Brownian motion of returns, Fund B has the favorable characteristic of successful growth, and should be selected.
In any case, the increasing rate of return manifests itself as variance in the Sharpe Ratio, and variance is a proxy for risk in the Markowitz mean-variance paradigm. This flavor of variability should be considered less risky, not more so. Accounting for second-order, rates of change of returns, is beyond the scope of this paper, reserved for a future follow-up. The purpose of showing this comparison is to highlight how funds of different characteristics can have identical average and standard deviation of returns.
Let's consider another set:
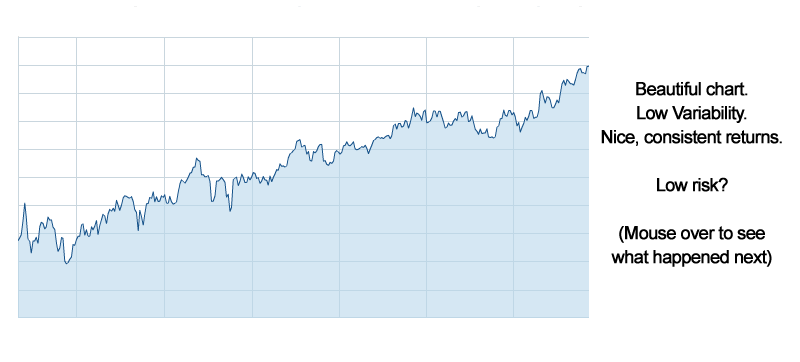
We could show many more examples of where the standard deviation of sub-periodic returns is a poor proxy for risk, but let's continue...
Solutions
Any solution we find should accomplish the following:1) Use a more accurate description of historic returns than the simple arithmetic mean (the numerator).
2) Find a more helpful characterization of risk than the standard deviation of past periodic returns (the denominator).
Solution #1 - The Numerator
A simple solution to address the issue with average returns above is to use compound returns. Instead of adding each periodic return from t=1 to T, we could just take the compound return at the end of the total period (t=T). Problem solved? Each fund or security would be scored linearly with its total compound return over the period. However, we would like to provide a scoring method which lends itself for ex-ante decisions, where we may want to match periodic returns to variance, or to use a Monte Carlo mechanism to determine probabilistic returns. For this reason, we want to keep the granularity of sub-periodic returns.Exponential Growth
Calculating simple returns as we have done above is easy:
$R = {P_e - P_b} / P_b$, or $R = {P_e / P_b} -1$
$R$
$P_e$
$P_b$
$P_e$
$P_b$
- Return (x100 = %)
- the price at the end of the period
- the price at the beginning of the period.
- the price at the end of the period
- the price at the beginning of the period.
$P_f = P_i (1 + R_1) (1 + R_2) ... (1 + R_n)$
$P_f$
$P_i$
$R_x$
$P_i$
$R_x$
- final Price
- initial Price
- Return for each sub-period.
- initial Price
- Return for each sub-period.
$P_f = P_i (1 + R_n) ^ n$
$P_f$
$P_i$
$R_n$
$n$
$P_i$
$R_n$
$n$
- final Price
- initial Price
- Rate of Return for each sub-period.
- number of sub-periods
- initial Price
- Rate of Return for each sub-period.
- number of sub-periods
Logarithmic Returns
Logarithmic returns measure the rate of exponential growth. Instead of measuring the percent of price change for each sub-period, we measure the exponent of its natural growth during that time. Later, we can add each sub-period's exponential growth to get the total growth for the period. The arithmetic for a single period then becomes:
$P_f = P_i e ^R$ , or $ln(P_f/P_i) = R$
$P_f$
$P_i$
$R$
$P_i$
$R$
- final Price
- initial Price
- Return for the period.
- initial Price
- Return for the period.
To sum logarithmic returns over several periods:
$R_{tot} ≡ {∑↖T↙{t=1} R_t}$
where $R_t = ln(P_t/P_{t-1})$
$ln(P_1/P_0) + ln(P_2/P_1) + ln(P_3/P_2) + ... + ln(P_T/P_{T-1})$
$ln(P_1) - ln(P_0) + ln(P_2) - ln(P_1) + ln(P_3) - ln(P_2) ... + ln(P_T) - ln(P_{T-1})$
$R_{tot} = ln(P_T) - ln(P_0)$
$R_{tot} = ln({P_T/P_0})$
So, an improved numerator would be the average (arithmetic mean) of logarithmic returns:
$R↖{-} = R_{tot}/T$
where $R_{tot} = ln(P_T/P_0) \;\;\;or\;\;\; {∑↖T↙{t=1} ln(P_t/P_{t-1})}$
This gives us a good weighting of the total compounded return for the period.
Normalizing Returns
In practice, it would be helpful if this measure appeared in our metric as the more commonly relatable annual return percentage. Investors simply are not familiar with judging sub-periodic returns, especially in logarithmic terms. For this reason, we normalize our return metric to an average annual return, as follows:
$R_{norm} ≡ (e^{R↖{-} T_{ann}} - 1) * 100$
$R_{norm}$
$R↖{-}$
$T_{ann}$
$R↖{-}$
$T_{ann}$
- normalized return (avg log return, normalized to simple annualized return)
- average sub-periodic logarithmic return
- Number of sub-periods in one year. (monthly=12, weekly ≈ 52, daily ≈ 252)
- average sub-periodic logarithmic return
- Number of sub-periods in one year. (monthly=12, weekly ≈ 52, daily ≈ 252)
Substituting logarithmic returns for simple arithmetic returns is an effective, easy-to-implement solution to the problems described in the numerator. This normalized return should be far more helpful to an investor than an average, sub-periodic, arithmetic return. Our improved numerator is this normalized total return, computed by adding the sub-periodic logarithmic returns, and converting to an annualized return.
Benchmark not required
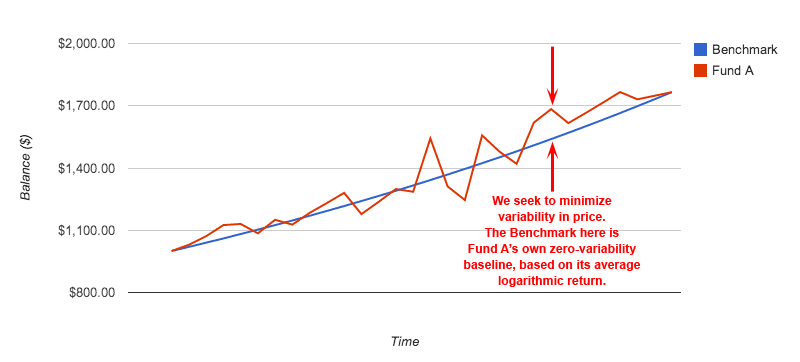
What are we missing? Notice the lack of reference to any benchmark fund. This approach may obviate the need for a separate benchmark fund in the analysis. In most cases, a risk-free fund serves simply as a zero, or near-zero, variability baseline from which to measure the variability of the fund under study. The mean logarithmic return demonstrates the zero-variability baseline for a fund of the same total return over the period. We can now measure variability of a fund's returns against its own average log return, as we will demonstrate below. Of course, one could still compare the sub-periodic log returns to the log returns of an external benchmark, if desired.Consider this fund:
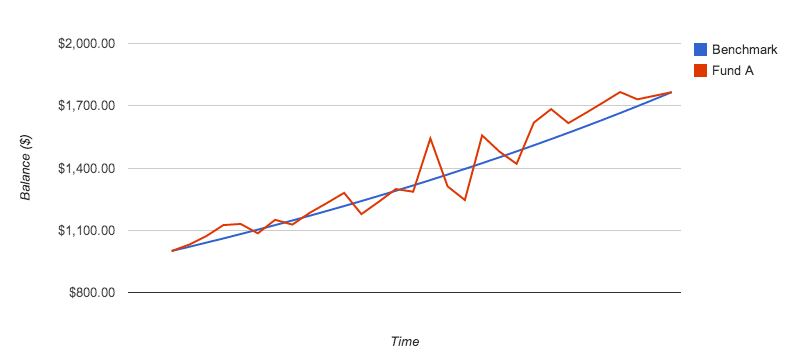
In this case, the benchmark for zero-variability is simply the same fund, had it remained at its average logarithmic rate of return for each period. This is an important characteristic as we move to solve the issues with the Ratio's denominator.
Solution #2 - The Denominator
Is Standard Deviation of returns the proper measure?
In a market where prices are set by crowds, variability is inevitable. Price variability may not be a good indicator of risk, but, should an investor seek to reduce variability? Overall return is the objective, and minimization of risk is, of course, also an objective. The risk/reward ratio is an important consideration in every investment decision. But most risk is, after all, unknowable. Do we simply find the most convenient proxy we can find for risk (variability), and use it in our decision-making? Variability looks scary, so should we try to avoid it? The answer may be "Yes".But, notice we are discussing variability in Price, not variability in Returns. This is an important distinction. The standard deviation of returns does not always properly measure the variability of price, which is our goal.
Why measure variability of price and not returns? Consider these funds:
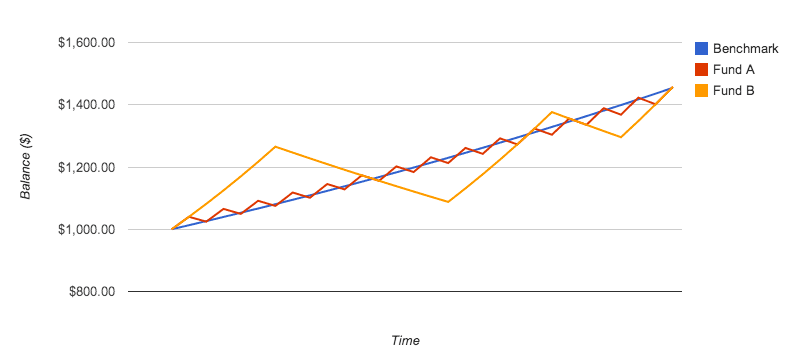
So, is the answer to simply substitute the standard deviation of price for the standard deviation of returns? Not so fast.
First, it is not the standard deviation of nominal prices that we seek to measure. A high growth fund will, by definition, have a high variability of price, while the only fund with zero variance will be a fund with zero return. What we must measure is the variability of the fund's price compared to the ideal: a fund with zero variability. Fortunately, by measuring the fund's logarithmic returns, we already have a zero-variability baseline for comparison: the same fund's periodic prices, had it earned it average logarithmic return during each sub-period, as discussed above. An elegant solution obviates the need for a separate benchmark fund, and uses its own zero-variability ideal as the benchmark, as shown here:
$P_n' ≡ P_i e ^{R↖{-}n}$
$P_n'$
$P_i$
$R↖{-}$
$n$
$P_i$
$R↖{-}$
$n$
- zero-variability Price at end of sub-period
- initial Price
- average logarithmic return
- number of sub-periods to this point
- initial Price
- average logarithmic return
- number of sub-periods to this point
The differential we want to measure is $P_n - P_n'$. But, so that we can compare funds at varying asset prices, we normalize this price differential to a ratio of the zero-variability price: $(P_n - P_n')/P_n'$, as follows
$D_t ≡ (P_n - P_i e ^{R↖{-}n}) / {P_i e ^{R↖{-}n}}$
or
$D_t ≡ P_n / {P_i e ^{R↖{-}n}} - 1$
or
$D_t ≡ P_n / {P_i e ^{R↖{-}n}} - 1$
$D_t$
$P_n$
$P_i$
$R↖{-}$
$n$
$P_n$
$P_i$
$R↖{-}$
$n$
- the differential price in period t, versus its zero-variability ideal price
- actual Price at end of sub-period
- initial Price
- average logarithmic return
- number of sub-periods to this point
- actual Price at end of sub-period
- initial Price
- average logarithmic return
- number of sub-periods to this point
So, we can calculate the standard deviation of this differential ($σ_D$) over the entire period, as follows:
$D↖{-} ≡ 1/T ∑↖T↙{t=1} D_t$
$D↖{-}$
- the average value (arithmetic mean) of the above price differentials
$σ_D ≡ √{{∑↖T↙{t=1} (D_t - D↖{-})^2}/{T-1}}$
$σ_D$
- standard deviation of price differentials
This standard deviation of price differentials provides more information than the standard deviation of arithmetic returns, especially if one uses variability as a proxy for risk. How far the price deviates from the ideal is far more important than a single sub-period's return.
Another advantage of this method is consistency across sub-periods of different length. When measuring the standard deviation of returns, the numbers are much smaller in shorter time periods than in longer. For example, the standard deviation of a fund using monthly returns will be many times higher than the standard deviation of daily returns. By measuring the standard deviation of price differentials, the difference in nominal prices for a day is similar in scale to the monthly or yearly price. Thus, the standard deviation numbers are more relatable, and less dependent on the time granularity chosen.
We now have a more valuable gauge of variability vis-a-vis risk. But, we still have one problem:
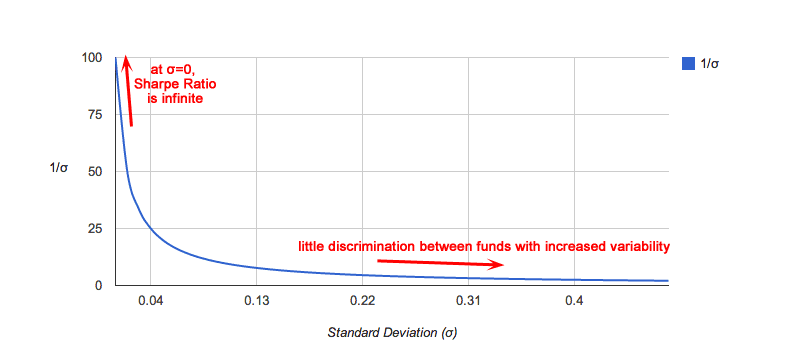
Standard Deviation ($σ$) does not belong in the denominator
Changes in the denominator move any ratio hyperbolically, obfuscating important information. As variability (as $σ$) goes to zero, the ratio becomes infinite, regardless of its return. Once variability increases past a certain point, the ratio provides less information about comparative variabilities between funds.The following chart demonstrates how changes in the Standard Deviation of returns, in the denominator, affects the Sharpe Ratio.
So, how do we weigh Price Variability?
If we structure the variability component of our measure to range from $0 → 1$, we could use this component as weighting multiplier (instead of divisor), and our measure would retain important information about the Return Rate, mapping closely to expected future returns. One way to accomplish a variability factor range between $0$ and $1$ would be to compare the standard deviation of the studied fund to the highest standard deviation in our universe of funds, or to the highest limit of variability we would accept. Here is such a weighting factor:Introducing the Variability-Weighted Return
$VWR \; ≡ \; R_{norm}(1-{(σ_P/σ_{max})^τ)$
for: $0 \;≦ \;σ_P \;≦ \;σ_{max}$
for: $0 \;≦ \;σ_P \;≦ \;σ_{max}$
$VWR$
$R_{norm}$
$σ_P$
$σ_{max}$
$τ$
$R_{norm}$
$σ_P$
$σ_{max}$
$τ$
- Here we introduce our new measure, the Variability-Weighted Return
- normalized return (avg log return, normalized to simple annualized return)
- standard deviation of price differentials
- maximum acceptable $σ_P$ (investor limit)
- rate at which weighting falls with increasing variability (investor tolerance)
- normalized return (avg log return, normalized to simple annualized return)
- standard deviation of price differentials
- maximum acceptable $σ_P$ (investor limit)
- rate at which weighting falls with increasing variability (investor tolerance)
If we choose the maximum acceptable Standard Deviation of price differentials ($σ_{max}$) and the exponent ($τ$), we can select a preferred weighting curve:
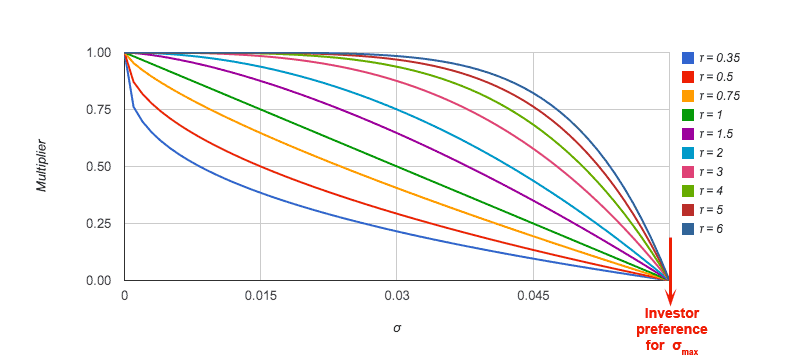
Now our measure, which we have dubbed the "Variability-Weighted Return", is the normalized logarithmic return times a multiplier, ranging from $0$ to $1$, that weights the fund's return by a factor corresponding to the investor's preference for price variability tolerance ($τ$). This new measure contains far more information than the Sharpe Ratio.
Based on our observations, the curve representing typical investor preference for variability is similar to the curve in this chart with the exponent ($τ$) between 2 and 3. Risk averse investors, such as those near or in retirement, may wish to choose a lower $σ_{max}$ and/or a risk tolerance ($τ$) of less than one.
Results
So, how did we do? Let's take a look at some charts, to see if these scores make sense. First a daily price chart:
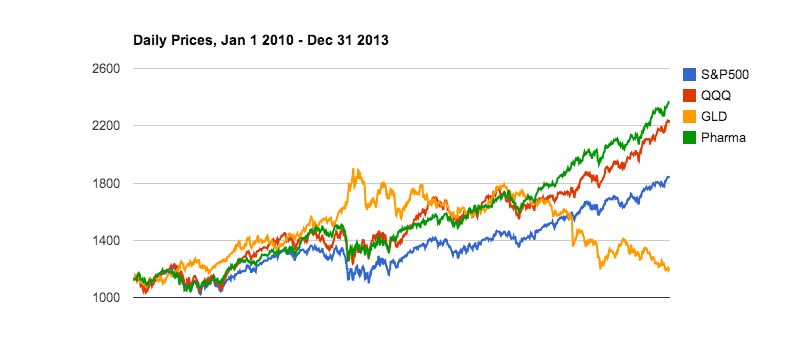
|
Fund
(2010-2013)
|
S&P 500 | QQQ | GLD | Pharma Fund | ||||
| $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | |
| Daily | 13.47 | 0.0514 | 19.02 | 0.0519 | 1.99 | 0.1704 | 20.74 | 0.0472 |
| Weekly | 13.40 | 0.0515 | 18.92 | 0.0527 | 1.98 | 0.1719 | 20.63 | 0.0473 |
| Monthly | 13.47 | 0.0513 | 19.02 | 0.0539 | 1.99 | 0.1721 | 20.74 | 0.0471 |
The first thing you may notice is that, unlike the values used in the Sharpe Ratio, the parameters we use are consistent for each fund, across daily, weekly, or monthly granularity. Properly normalized returns would be identical for each sub-period length. However, in our case, we used $52$ as the number of weeks per year, when, in our sample, we had $52.25$ weeks per year ($209$ sub-periods to cover all 4 years, with weekly closes). We used $251.5$ trading days per year, which was correct during these 4 years.
Before we continue, let's take a closer look at the 4 funds above, in relation to their zero-variability baselines, so their price variabilities become more obvious:
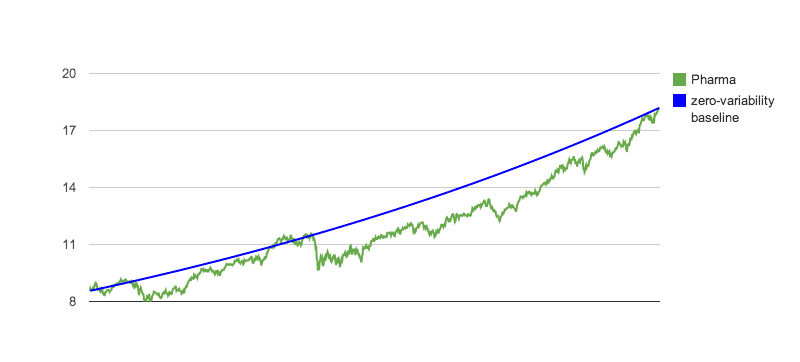
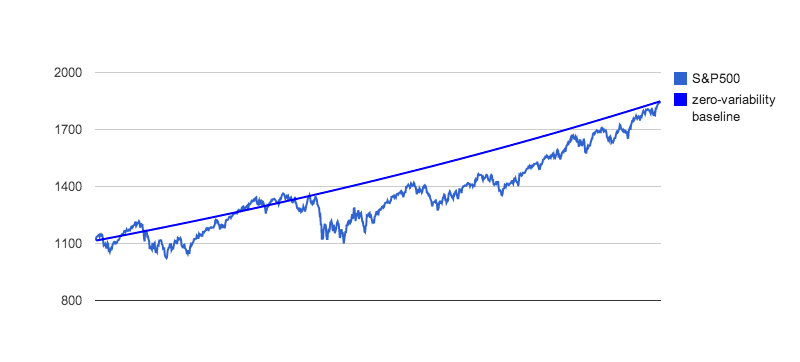
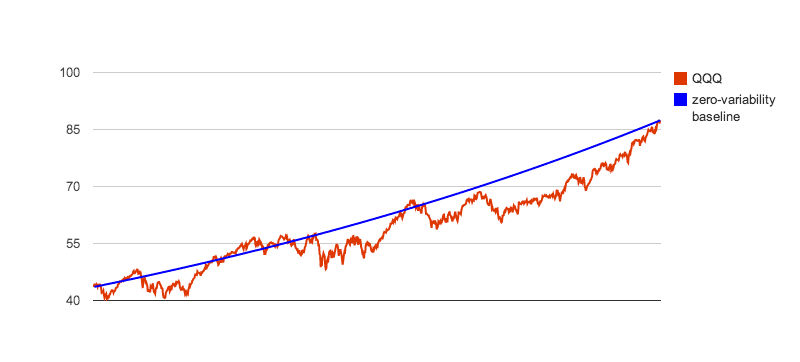
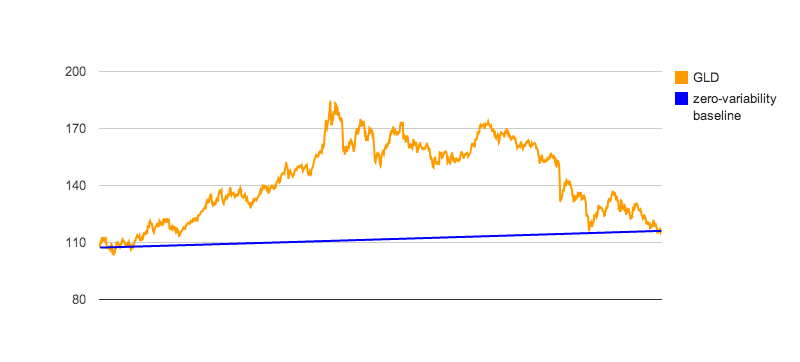
|
Fund
(2010-2013)
$σ_{max}$ = 0.19, $τ$ = 2
|
S&P 500 | QQQ | GLD | Pharma Fund | ||||||||||||||||
| Daily |
|
|
|
|
||||||||||||||||
| Weekly |
|
|
|
|
||||||||||||||||
| Monthly |
|
|
|
|
Which values are more meaningful? When a person tells us that a fund has a Sharpe Ratio of 0.0159, what does that tell us? First, we must ask what was used for the benchmark in the calculations. Then, we must ask about the granularity used. Did they use daily values? Weekly? Monthly? Yearly? Even then, what does 0.0159 mean? With the Variability Weighted Return (VWR), we at least can relate the value to an annual return rate, attenuated for variability. In the case of the funds above, the Sharpe Ratio did put the funds in our order of preference, but what if we change our preferences, or the funds we are considering have a greater disparity of variability?
Notes: GLD has poor returns over this period, as well as the highest variability in the group. So, it rightfully scores at the lowest value. Since its $σ_P$ is very close to the $σ_{max}$ we have chosen, it will score close to zero, regardless of return. The pharmaceutical fund has the highest return and, remarkably, the lowest $σ_P$ over this period. So, it is properly scored at the highest of the set. But, what if our preferences change? Here is an interactive tool to use to experiment with $σ_{max}$ and $τ$ values, to see how the affect the scoring:
Below, we show an example where the Sharpe Ratio fails in properly scoring the funds. Consider the following funds, in a weekly chart from 2010-2013:
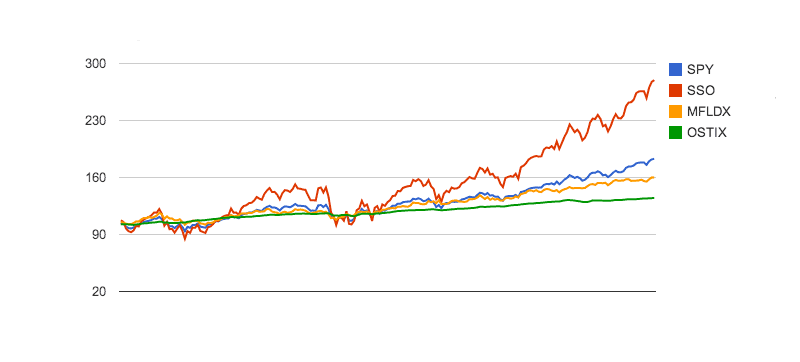
We find the Sharpe Ratio values completely unhelpful here. Practically no discrimination is made between the low-return, low-volatility fund MFLDX, and the high-return, high-volatility fund SSO, even though these funds have wildly different characteristics. This is one of the problems inherent in using a ratio. Using the Sharpe Ratio, little discrimination is made between SPY and its 2x ETF cousin, SSO. Because of its extremely low volatility (See: Standard Deviation ($σ$) does not belong in the denominator, above), the short-term bond fund OSTIX has a Sharpe Ratio of more than double the next closest fund, while few investors would have preferred this fund over this period of time. Using the VWR, the scores fall in line with expectations, and one can adjust the preferences to penalize more heavily the volatility of SSO and SPY. No such adjustments are available with Sharpe.
Let's take a closer look, so we can understand why the Sharpe Ratio is nearly identical for SSO and MFLDX:
|
Fund
(2010-2013)
|
SPY | SSO | MFLDX | OSTIX | ||||
|
VWR Parameters |
$R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ |
| 15.82 | 0.05149 | 28.77 | 0.10222 | 12.00 | 0.03622 | 7.29 | 0.01286 | |
|
Sharpe Parameters |
$R↖{-}$ | $σ_D$ | $R↖{-}$ | $σ_D$ | $R↖{-}$ | $σ_D$ | $R↖{-}$ | $σ_D$ |
| 0.00252 | 0.02190 | 0.00529 | 0.04394 | 0.00175 | 0.01449 | 0.00082 | 0.00322 | |
As you can see, SSO had an $R↖{-}$ which was 3.02 times that of MFLDX. But, it also had a $σ_D$ which was 3.03 times that of MFLDX. Thus, their Sharpe Ratios are nearly identical. We find the inability of the Sharpe ratio to distinguish between these 2 vastly different funds troubling, as this could lead investors to make choices which do not well serve their portfolios. $R↖{-}$ for OSTIX approached zero during this period. But, its Sharpe denominator $σ_D$ also approached zero, launching its Sharpe Ratio to the highest of the group. Across this group of funds, the Sharpe Ratio has mislead the investor into incorrect scoring. The VWR allows investors to choose weighting preferences for returns versus variability, which can more accurately target their desired performance.
OK, one last chart. Let's take a look at the same funds, over a period which contains a market correction, to see how the indicators perform under more difficult conditions. Here are the same four funds, from 2008-2013:
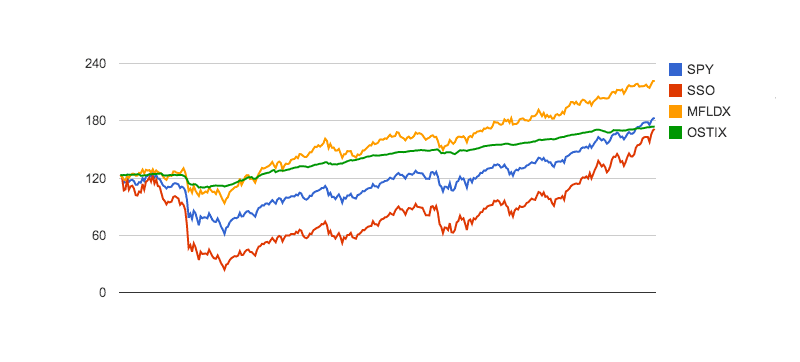
Again, the VWR does a much better job of scoring these funds than does the Sharpe Ratio. Note that, because its $σ_P$ value, at 0.19107, was higher than the limit set in our preferences, SSO scored a zero using the VWR method. Using Sharpe, SSO and SPY were virtually indistinguishable, and OSTIX still scores higher than the best fund of the group.
HINT: If you wish to consider funds with the variability of SSO, change the $σ_{max}$ value in the utility above to 0.2 or higher. Then, adjust the $τ$ value to change your preference for variability weighting. As you will see, VWR scores these funds in a much more valuable manner. Here are the $R_{norm}$ and $σ_P$ values for your review:
|
Fund
(2008-2013)
|
SPY | SSO | MFLDX | OSTIX | ||||
|
VWR Parameters |
$R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ | $R_{norm}$ | $σ_P$ |
| 6.83 | 0.11375 | 5.67 | 0.19107 | 10.29 | 0.06618 | 5.93 | 0.04334 | |
|
Sharpe Parameters |
$R↖{-}$ | $σ_D$ | $R↖{-}$ | $σ_D$ | $R↖{-}$ | $σ_D$ | $R↖{-}$ | $σ_D$ |
| 0.00121 | 0.03048 | 0.00235 | 0.05970 | 0.00156 | 0.02030 | 0.00059 | 0.00492 | |
Summary
$VWR \; ≡ \; R_{norm}(1-{(σ_P/σ_{max})^τ)$
for: $0 \;≦ \;σ_P \;≦ \;σ_{max}$
for: $0 \;≦ \;σ_P \;≦ \;σ_{max}$
$VWR$
$R_{norm}$
$σ_P$
$σ_{max}$
$τ$
$R_{norm}$
$σ_P$
$σ_{max}$
$τ$
- the Variability-Weighted Return
- normalized return (avg log return, normalized to simple annualized return)
- standard deviation of price differentials
- maximum acceptable $σ_P$ (investor limit)
- rate at which weighting falls with increasing variability (investor tolerance)
- normalized return (avg log return, normalized to simple annualized return)
- standard deviation of price differentials
- maximum acceptable $σ_P$ (investor limit)
- rate at which weighting falls with increasing variability (investor tolerance)
What is proposed here is a more practical method of scoring funds, based on actual compounded returns and weighting for price variability. It overcomes some of the fundamental problems inherent in the Sharpe Ratio. Our new method, Variability-Weighted Return (VWR) provides the following improvements:
- Weighting for returns is now representative of actual compounded returns.
- Weighting for variability in price is a better proxy for risk than variability in sub-periodic returns.
- Weighting for variability now matches observed investor behavior vis-a-vis price variability as risk.
- Weighting for variability can now be customized per investor preferences.
- Comparison to a benchmark fund is not required.
- Scoring is less dependent upon granularity of samples (time per sub-period), and more easily comparable to others.
We would love to hear your comments. Email Us

